Simulating Turing Machines with Wang tiles

1st May, 2023

Simulating Turing Machines with Wang tiles

Wang tiles are squared tiles with colored edges. They cannot be rotated but can be assembled into tilings, with touching edges having the same color.

1964, Hao Wang' student Robert Berger showed that the "Domino Problem" is undecidable [1], ie no algorithm can tell whether or not a specific tileset can tile the plane from a given initial configuration.

The proof consists in generating a specific tileset for any Turing machine, such that the initial configuration yields a tiling if and only if the machine never halts. As the Halting Problem is undecidable, so too is the Domino Problem.

wtm (Wang tiles Turing Machine) is a Python program that demonstrates how to perform computation by simulating a Turing machine (TM) with Wang tiles. It is based on the procedure described by Robinson in 1971 [2].

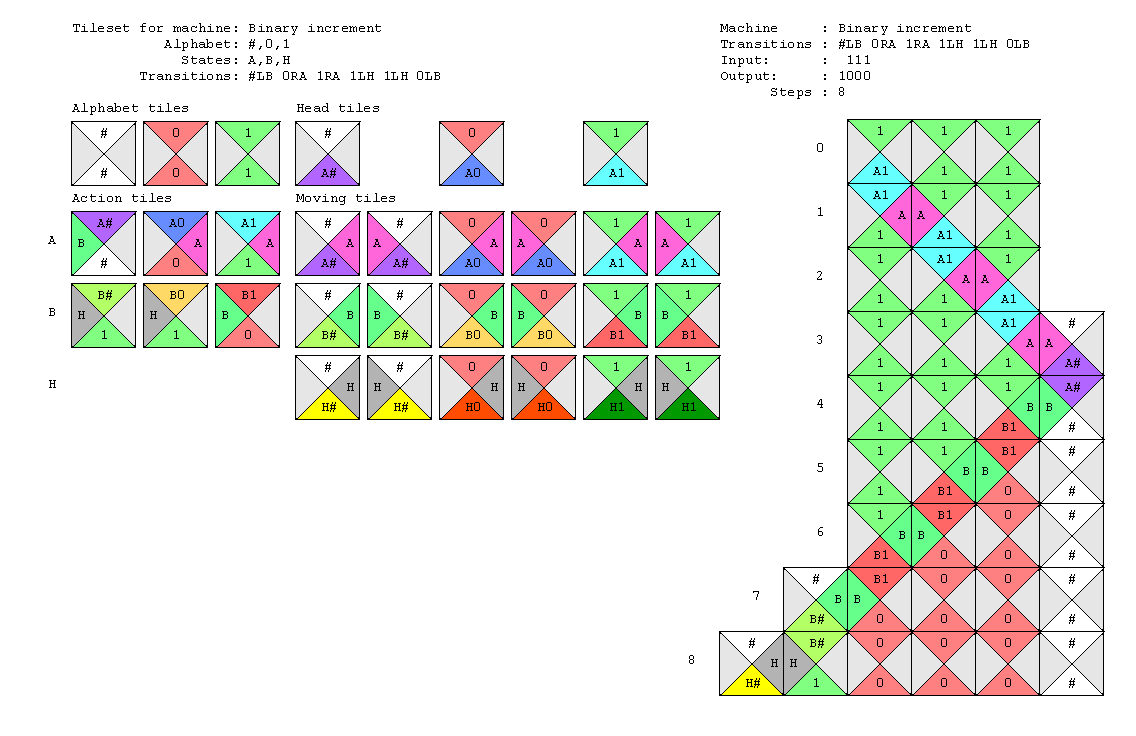
Here is a typical output from wtm. Given a Turing machine and an input, wtm generates an image with the tileset on the left and the computation on the right. Here, the machine increments a binary number. At the top of the tiling, we can read the input 111. The result 1000 appears at the bottom, after the computation steps are over.

Here is another image for another machine, a binary adder computing 101 + 11 = 1000: wtm_binary_adder.png.

How does it work? wtm generates a specific tileset for each machine. Each tileset encodes the machine alphabet, states and transitions. Each configuration of the machine is simulated with a row of Wang tiles, and each machine step grows the tiling downwards. Tilesets are such that procedurally tiling a new row simulates the execution of the machine.

Some tiles have colors on their south edge that do not appear on any north edge. Consequently, whenever these tiles are used, the tiling cannot continue and the machine halts. The output of the computation can then be read on the last row.

In summary, wtm does:

encode a Turing machine into a set of Wang tiles
run the machine for a given input
draw the tiling that results from the computation

wtm source code is available on https://github.com/nst/WangTilesTuringMachines/.

The Busy Beaver Game

In 1962, Hugarian mathematician Tibor Radò posed a challenged to the readers of the Bell System Technical Journal. Considering a binary Turing machine (TM) (alphabet = {1}, blank symbol = 0), for how long can such a machine run before halting?

Radó’ student Shen Lin proved that BB-3 = 21, ie no binary TM with 3 states will halt after more than 21 steps.

wtm can produce tilesets and tilings for such "Busy Beavers", as for any other Turing machine. Here are outputs of 2-symbols Busy Beavers with 2, 3 and 4 states (click to enlarge).

Busy Beavers in Theroretical Computer Science

Busy beavers is an interesting problem to study because it is undecidable. There's no algorithm to find BB-k. Additionally, S(k) grows very quickly with k [4], considering the following definitions:

S(k): max number of steps before halting for a binary TM with n states, starting from a blank tape
Sigma(k): max number of ones left on the tape by such a machine

BB-States	S(k)	Sigma(k)
BB-2	6 (Rado, 1962)	4
BB-3	21 (Lin and Rado, 1965)	6
BB-4	107 (Brady, 1983)	13
BB-5	>= 47,176,870	>= 4098
BB-6	7.4 × 10^36,534

Finding Busy Beavers is a fun theoretical computer science problem, but is also a tool used to measure the difficulty of solving some famous conjectures.

In a fascinating article [5], Quanta magazine explains how Turing machines can be defined so that, by halting or not after a certain number of steps, they will tell if the conjecture is right or wrong. For instance:

The Goldbach conjecture – Is every even integer greater than 2 is the sum of two primes or not? In 2015, an anonymous GitHub user published [6] a 27 states Turing machine that will prove the conjecture right or wrong if halting or continuing after BB-27 steps.
The Riemann hypothesis – In 2016, Aaronson and others have specified a binary Turing machine that will halt in BB(744) steps if on only if the Riemann hypothesis is false.
The ZF set theory – Is the ZF (Zermelo-Fraenkel) set theory consistent? In 2016, Aaronson and his graduate student Adam Yedidia have specified a binary Turing machine that would prove that the axiomatic system underpinning modern maths is inconsistent if and only if the machine halts after BB-7910 steps. O’Rear subsequently devised a much simpler 748 rule machine achieving the same purpose. Other mathematicians suspect that the number of rules can be brought down to maybe 50.

A minimal Turing machine in C

My Python implementation is fine to generate tilings, but it is super inefficient to study busy beavers with more than a few hundreds steps. So I wrote this minimal Turing machine in C:

fast and concise
no fancy datastructure, program is kept on input string
no need of state variable, instruction pointer moves as needed
assumes input in normal form

// Tiny Turing machine in C
// for 2-symbols Busy Beavers
// Nicolas Seriot, 2023-05-07

#include <stdlib.h>
#include <stdio.h>

#define TAPE_LEN 50000
#define MAX_COUNT 100000000

int runMachine(_Bool *t, char *p) {
   int h = TAPE_LEN/2;
   int i = 0; // instruction pointer
   int c = 0; // counter

   while (++c) {
      t[h] = p[i]-'0';      // write tape
      h+=p[i+1]=='R'?1:-1;  // move head
      if(p[i+2]=='H')break; // halt if needed
      if(h==0||h==TAPE_LEN-1){return -1;} // out of tape
      if(c==MAX_COUNT){return -2;} // max count reached
      i = 8*(p[i+2]-'A')+4*t[h];   // set ip for next state
   }
   return c;
}

int main(int argc, const char * argv[]) {    
   char *program = "1LB 1RC 1LC 1LB 1LD 0RE 1RA 1RD 1LH 0RA";
   int64_t sigma = 0;
   _Bool tape[TAPE_LEN] = {0};
   printf("* Tiny Turing Machine *\n");
   printf("Program: %s\n", program);
   int c = runMachine(tape, program);
   for (int i = 0; i < TAPE_LEN; i++) {sigma += tape[i];}
   printf("S = %d, Sigma = %llu\n", c, sigma);
   return 0;
}

Gist: https://gist.github.com/nst/0da460d9354fb591ce2255c778d6e680

Benchmarks:

% time python3 wtm_sandbox.py
S: 47176870
python3 wtm_sandbox.py  131.55s user 0.06s system 99% cpu 2:11.64 total

% time ./ttm
* Tiny Turing Machine *
Program: 1LB 1RC 1LC 1LB 1LD 0RE 1RA 1RD 1LH 0RA
S = 47176870, Sigma = 4098
./ttm  0.54s user 0.00s system 99% cpu 0.540 total

Conclusion

I've written the wtm program to generate tilesets for any Turing machine. Starting from any given input, the program will use the tiles to achieve computation deterministically.

I've shared various images of tiles performing binary additions and busy beavers. I've also discussed the profound theoretical implications of seemingly futile mathematical games.

Finally, I've written a minimal and concise Turing machine for 2-symbols Busy beavers.

[1] Berger, R. (1966). The undecidability of the domino problem (No. 66). American Mathematical Soc..

[2] Robinson, R. M. (1971). Undecidability and nonperiodicity for tilings of the plane. Inventiones mathematicae, 12, 177-209.

[3] Rado, T. (1962). On non‐computable functions. Bell System Technical Journal, 41(3), 877-884.

[4] Pascal Michel, The Busy Beaver Competitions, Institut de Mathématiques de Jussieu-Paris Rive Gauche

[5] John Pavlus, How the Slowest Computer Programs Illuminate Math’s Fundamental Limits, Quanta Magazine, December 10, 2020

[6] file-source27-txt, GitHub https://gist.github.com/anonymous/a64213f391339236c2fe31f8749a0df6