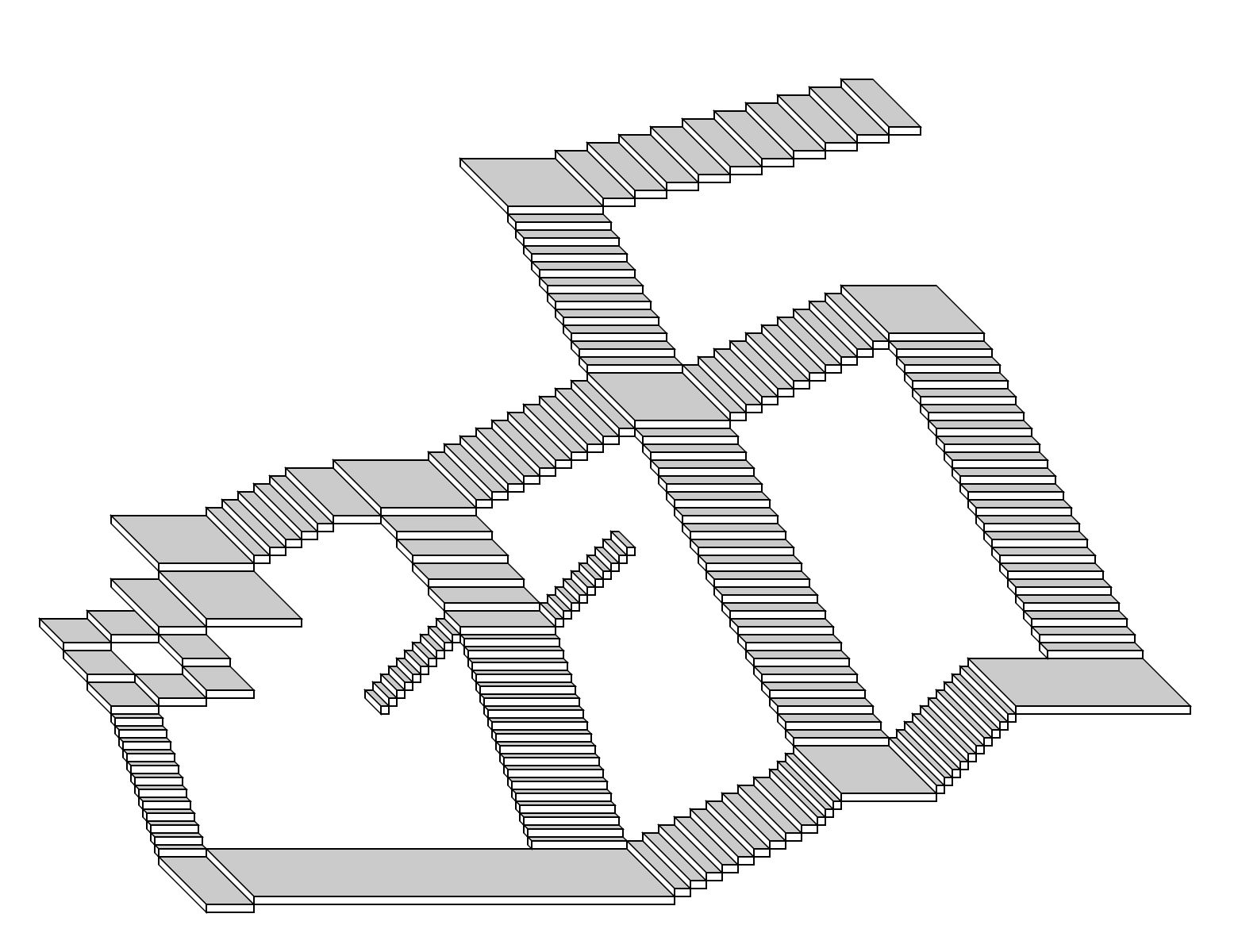
Drawing isometric stairs in Postscript
2022-10
I stubled upon this image.
Wondering how do to something similar in minimal Postscript, I came up with the following result in 11 lines (tweet).
<</PageSize[800 600]>>setpagedevice/S 5 def/f{/M exch def/C exch def/h exch def
/w exch def gsave M concat C setgray 0 0 w h rectfill 0 setgray 0 0 w h
rectstroke grestore}def/b{/H exch def/W exch def gsave W H 2 div 0.8[1 0 -1 1 0
S]f W S 1[1 0 0 1 0 0]f H 2 div S 1[-1 1 0 1 0 0]f grestore}def/U{/H2 exch def{
H 2 div neg H 2 div S add translate W H2 b}repeat}def/D{/H exch def{H 2 div H 2
div neg S sub translate W H b}repeat}def/L{/W2 exch def{W2 neg S neg translate
W2 H b}repeat}def/R{/W2 exch def{W S translate W2 H b}repeat}def/s{save}def/r{
restore}def/W 60 def/H 60 def 100 200 translate 2 30 L 2 30 D s 12 5 D 1 60 D 1
265 R 9 10 R 4 5 R r 2 30 R 1 30 U 1 60 U 1 60 R 1 60 U 5 10 R 1 30 R 1 60 R s
5 20 D s 10 5 L r s 18 5 D r 10 5 R r 10 10 R 1 60 R s 20 10 D 1 60 D 10 5 R 1
110 R r s 10 10 U 1 60 U 10 20 R r 10 10 R 1 60 R 20 10 D
A colleague of mine asked whether I worked for Poudlard, so here is a short walk-though of the full, expanded Postscript code stairs_full.ps.
First, we set the size of the page, no wonder.
<< /PageSize [780 600] >> setpagedevice
We set the height of steps.
/S 5 def
We now define a procedure to draw a face of a brick.
It takes 4 parameters on the stack: width, height, gray level, and a tranformation matrix.
/f {
/M exch def
/C exch def
/h exch def
/w exch def
gsave
M concat
C setgray
0 0 w h rectfill
0 setgray
0 0 w h rectstroke
grestore
} def
We now define a procedure to draw a brick, ie its 3 faces.
The procedure takes 2 parameters on the stack: the width and height of the brick.
The procedure calls the f procedure that we've previously definded, with a transformation matrix for each of the three faces.
/b {
/H exch def
/W exch def
gsave
W H 2 div 0.8 [ 1 0 -1 1 0 S ] f
W S 1 [ 1 0 0 1 0 0 ] f
H 2 div S 1 [ -1 1 0 1 0 0 ] f
grestore
} def
We now define the Up (U), Down (D), Left (L) and Right (R) procedures.
Each take 2 parameters on the stack: length and number of repeats.
Each of these procedures moves to the position where to draw the new brick (lower left corner) and repeatedly call the b procedure to draw several ones if needed.
/U { /H2 exch def { H 2 div neg H 2 div S add translate W H2 b } repeat } def
/D { /H exch def { H 2 div H 2 div neg S sub translate W H b } repeat } def
/L { /W2 exch def { W2 neg S neg translate W2 H b } repeat } def
/R { /W2 exch def { W S translate W2 H b } repeat } def
Now we have defined the two procedures that we need.
We can set the initial width and height of the bricks.
/W 30 def /H 30 def
We set the coordinates of the initial brick.
100 200 translate
And now we can call our U D L R procedures with the required lenght and repeat parameters.
We start with 2 bricks of width 30 to the left, and so on.
2 30 L 2 30 D
The save and restore operators will save and restore the whole context, including variables H and W.
In practice, the drawing goes on from the point of the last save.
save
12 5 D
1 60 D
1 265 R
9 10 R
4 5 R
restore
The remaining code is now straightforward.
2 30 R
1 30 U
1 60 U
1 60 R
1 60 U
5 10 R
1 30 R
1 60 R
save
5 20 D
save
10 5 L
restore
save
18 5 D
restore
10 5 R
restore
10 10 R
1 60 R
save
20 10 D
1 60 D
10 5 R
1 110 R
restore
save
10 10 U
1 60 U
10 20 R
restore
save
10 10 R
1 60 R
20 10 D
restore
The elegance and conciseness of this code is partly due to transformation matrices and stacked context savings. These combined techniques free us from explicitely keeping track of x y z coordinates.
"At first, it looks complicated. But when you explain, it's easy!" (Émilien, 10 yo)