
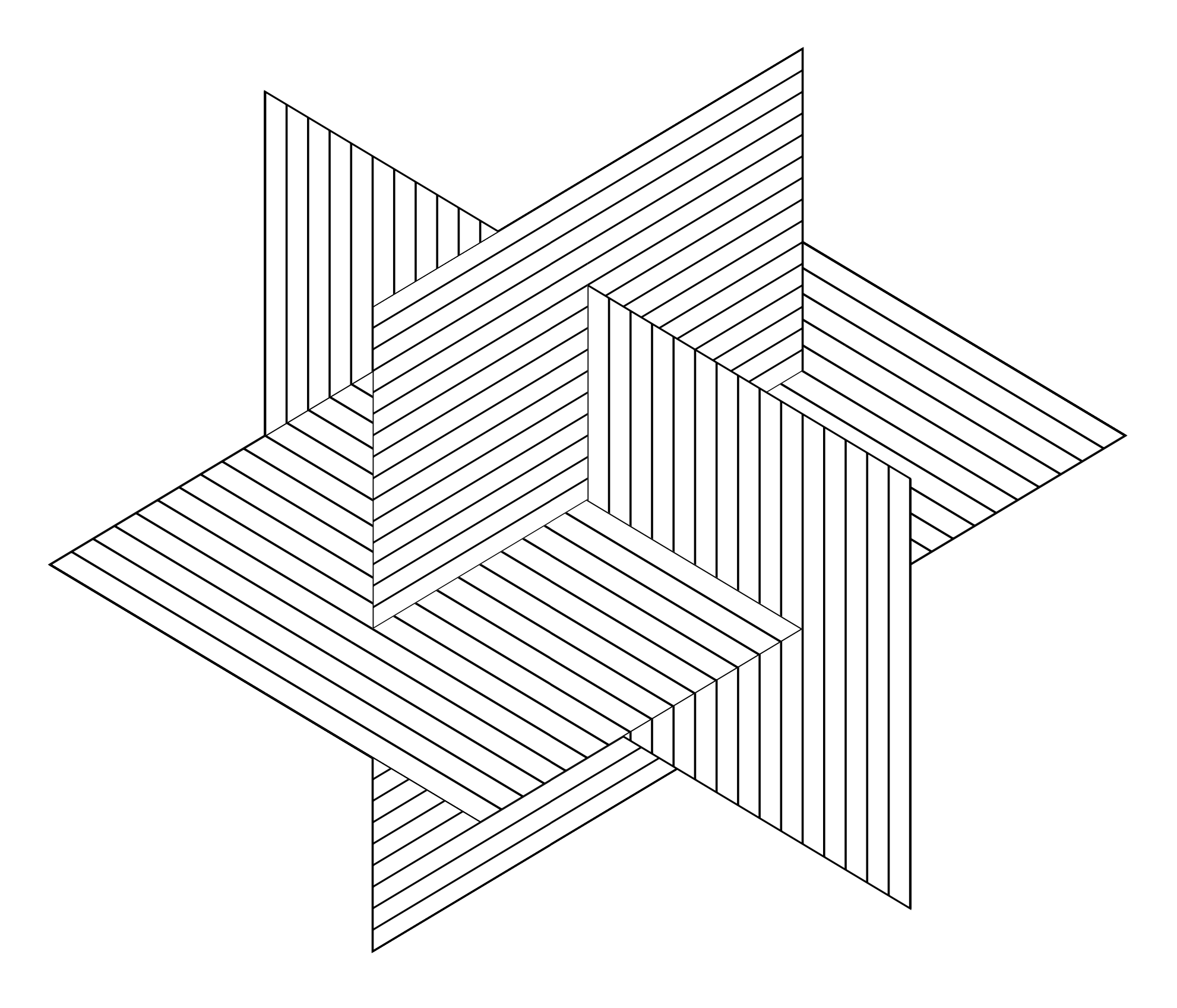
Reproducing an image with intersecting planes in Postscript
2022-10
My attention was drawn by this image from @nico_vdw_art. The image is interesting because plans intersect and overlap. My goal was to reproduce this image with code, as elegantly as possible. I ended up with the following, minimal, 389 bytes Postscript code. This article explains how.


%!PS
200 200 translate/W 300 def/H 200 def/w 150 def/h 100 def/P{1 setgray 0 0 W H
rectfill 0 setgray 0 0 W H rectstroke 0 10 W{dup 0 moveto H lineto}for stroke}
def/A[1 0.6 -1 0.6 50 60]def/B[0 1 1 0.6 0 0]def/C[1 -0.6 0 1 -50 200]def/p{
gsave concat exec P grestore}def 1 0 0{}A p 0 1 0{}B p 1 0 0{0 0 W h rectclip}A
p 0 0 1{}C p 1 0 0{0 0 w H rectclip}A p 0 1 0{w 0 w h rectclip}B p showpage
Original Image: https://twitter.com/nico_vdw_art/status/1559017582174298112
My tweet: https://twitter.com/nst021/status/1578094107947302926
Gist: https://gist.github.com/nst/4f2f04f06fbf6b1c7518b45e2899df15
There will be 2 different approaches, plus the "golfing" part where I make the code as small as possible.
My first approach was to:
Here are the drawing steps and the source code.
Note that I've added R G B colors to help identifying which lines draws what.

The drawing is done, but not elegantly. There are way too many hardcoded magic numbers. Additionally, there MUST be a way to draw less planes, ie to call procedure P less than 12 times.
%!PS
300 500 translate
/L 160 def
/L2 L 2 div def
/P {
1 setgray
0 0 L2 L rectfill
setrgbcolor % r g b
newpath
0 0 moveto
0 L lineto
L2 L lineto
0 10 L {
dup
0 exch moveto
L2 exch lineto
} for
stroke
} def
% [a b c d tx ty]
% x = ax + cy + tx
% y = bx + dy + ty
0 1 0 gsave [ 1 0.6 0 1 L2 neg L2 -3 mul 16 add] concat P grestore
0 1 0 gsave [-1 -0.6 0 1 L2 L2 -2 mul 32 add] concat P grestore
1 0 0 gsave [-1 0.6 1 0.6 75 L2 neg 15 add ] concat P grestore
1 0 0 gsave [ 1 -0.6 -1 -0.6 L2 5 sub L 33 sub ] concat P grestore
0 0 1 gsave [ 0 -1 1 -0.6 L2 -2 mul L2 2 mul ] concat P grestore
0 0 1 gsave [ 0 1 1 -0.6 L2 -2 mul 0 ] concat P grestore
1 0 0 gsave [ 1 -0.6 -1 -0.6 L2 neg 32 ] concat P grestore
0 1 0 gsave [ 1 0.6 0 1 L2 neg L2 neg 16 add ] concat P grestore
0 1 0 gsave [-1 -0.6 0 1 L2 32 ] concat P grestore
0 0 1 gsave [ 0 -1 1 -0.6 0 L2 16 sub ] concat P grestore
0 0 1 gsave [ 0 1 1 -0.6 0 -96 ] concat P grestore
1 0 0 gsave [-1 0.6 1 0.6 L2 neg L neg ] concat P grestore
showpage
My second take was to:
Here are the code and the drawing steps. Not only we only call P 6 times instead of 12, but we also need only three tranformation matrices instead of 12.

%!PS
200 200 translate
/W 300 def
/H 200 def
/W2 W 2 div def
/H2 H 2 div def
/P {
1 setgray
0 0 W H rectfill
setrgbcolor % r g b
0 0 W H rectstroke
0 10 W {
dup
0 moveto
H lineto
} for
stroke
} def
% [a b c d tx ty]
% x = ax + cy + tx
% y = bx + dy + ty
/MR [ 1 0.6 -1 0.6 50 60 ] def
/MG [ 0 1 1 0.6 0 0 ] def
/MB [ 1 -0.6 0 1 -50 200 ] def
1 0 0 gsave MR concat P grestore
0 1 0 gsave MG concat P grestore
1 0 0 gsave MR concat 0 0 W H2 rectclip P grestore
0 0 1 gsave MB concat P grestore
1 0 0 gsave MR concat 0 0 W2 H rectclip P grestore
0 1 0 gsave MG concat 150 0 W2 H2 rectclip P grestore
showpage
In this last step, we don't change the logic, but only reduce the size of the code. We remove the colors. We refactor the code by creating a p procedure that draws the plane, but that also takes two operands: a tranformation matrix, and a block of code, that will either be empty or define a clipping region.
%!PS
200 200 translate
/W 300 def
/H 200 def
/W2 W 2 div def
/H2 H 2 div def
/P {
1 setgray 0 0 W H rectfill
0 setgray 0 0 W H rectstroke
0 10 W { dup 0 moveto H lineto } for
stroke
} def
/MR [ 1 0.6 -1 0.6 50 60 ] def
/MG [ 0 1 1 0.6 0 0 ] def
/MB [ 1 -0.6 0 1 -50 200 ] def
/p { gsave concat exec P grestore } def % {} M
{ } MR p
{ } MG p
{ 0 0 W H2 rectclip } MR p
{ } MB p
{ 0 0 W2 H rectclip } MR p
{ W2 0 W2 H2 rectclip } MG p
showpage
And now we shorten the names, remove white spaces, and we end up with the following 5 lines:
200 200 translate/W 300 def/H 200 def/w 150 def/h 100 def/P{1 setgray 0 0 W H
rectfill 0 setgray 0 0 W H rectstroke 0 10 W{dup 0 moveto H lineto}for stroke}
def/A[1 0.6 -1 0.6 50 60]def/B[0 1 1 0.6 0 0]def/C[1 -0.6 0 1 -50 200]def/p{
gsave concat exec P grestore}def 1 0 0{}A p 0 1 0{}B p 1 0 0{0 0 W h rectclip}A
p 0 0 1{}C p 1 0 0{0 0 w H rectclip}A p 0 1 0{w 0 w h rectclip}B p showpage